咱们简单从 what、why、how三方面进行介绍~
what:一句话介绍
咱们一句话介绍:LSTM,全名是「长短期记忆网络」(Long Short-Term Memory),是一种特殊的人工神经网络,主要用来处理和预测时间序列数据(就是那些有时间顺序的数据,比如天气预报、股市行情等)。
why:为什么需要 LSTM
其次,咱们要明白,为什么需要LSTM。
传统的神经网络在处理时间序列数据时有个很大的问题:它们记不住长期的依赖关系。举个例子,如果你在看一部电视剧,前几集提到的一个重要线索在后面几集才会揭示它的意义。普通神经网络就像是有点健忘的观众,只能记住最近几集的内容,早前的线索都忘了。而LSTM就像是一个记性很好的观众,它能够记住前面提到的重要细节,并在需要的时候利用这些信息。
how:LSTM 怎么做到
LSTM 是怎么做到的?
LSTM 通过一个巧妙的设计,让网络能够记住之前的信息,并且在合适的时候把这些信息传递下去。具体来说,LSTM 有几个特殊的「门」(gate)来控制信息的流动:
1. 遗忘门(Forget Gate):决定要忘记哪些信息。比如,不重要的剧情细节可以被遗忘。
2. 输入门(Input Gate):决定要记住哪些新的信息。比如,新出现的重要线索要记住。
3. 输出门(Output Gate):决定输出哪些信息。比如,根据前面的情节做出预测或解释当前情节。
通过这三个门的控制,LSTM 能够在时间序列数据中选择性地记住和忘记信息,从而在需要的时候准确地做出预测或分类。
一个简单的例子
想象一下,你在学习一门语言。刚开始学的时候,你会记住很多新的单词和语法(输入门打开),但随着学习的深入,你会逐渐忘记那些不常用的单词和语法(遗忘门打开)。当你在用这门语言交流时,你会根据上下文选择性地使用你记住的单词和语法(输出门打开)。
LSTM 就像是这样一个学习过程,能够灵活地记住重要信息并在需要的时候使用这些信息。
理论基础
数学原理与公式推导
LSTM的核心是通过引入不同的“门”机制来控制信息的流动。这些“门”包括遗忘门、输入门和输出门。
遗忘门
遗忘门决定了哪些信息需要丢弃。它的输出是一个介于0和1之间的向量,表示每个单元状态应该保留多少信息。
输入门
输入门决定了哪些新的信息需要存储到单元状态中。
接着,会生成候选单元状态,它表示可以加入到单元状态中的新信息。
更新单元状态
通过遗忘门和输入门来更新单元状态。
输出门
输出门决定当前单元状态的哪部分需要输出,并且通过一个激活函数(通常是tanh)处理后的结果作为输出。
公式说明:
- :当前时刻的输入。
- :前一时刻的隐状态。
- :当前时刻的单元状态。
- :前一时刻的单元状态。
- :当前时刻的候选单元状态。
- :遗忘门的激活值。
- :输入门的激活值。
- :输出门的激活值。
- :表示sigmoid激活函数。
- :表示tanh激活函数。
- :权重矩阵。
- :偏置向量。
算法流程
1. 输入预处理:
2. 计算遗忘门:
3. 计算输入门:
4. 计算候选单元状态:
5. 更新单元状态:
6. 计算输出门:
7. 计算当前时刻的隐状态:
- 通过输出门的结果和更新后的单元状态计算当前时刻的隐状态 。
- 。
通过遗忘门、输入门和输出门的机制,LSTM能够有效地记住重要信息,忘记不必要的信息,从而在处理长时间依赖的序列数据时表现出色。每一个时间步的计算过程相对复杂,但通过这些步骤,LSTM可以在保持长期记忆和处理当前输入之间找到平衡。
一个完整案例
这里,咱们给到大家一个完整的、详细的LSTM应用示例。
这个案例中,使用电力消费数据集,该数据集包含自2011年开始的每小时电力消耗数据。目标是根据历史数据预测未来的电力消耗。
整个代码是完整的,大家可以粘贴在自己的编译器中进行调试,同时也做了很完整的注释供大家学习~
数据集下载与预处理
大家可后台回复,“数据集”即可获取所有的数据集~
使用 pandas 处理数据。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 下载并读取数据
df = pd.read_csv('LD2011_2014.txt', sep=';', index_col=0, parse_dates=True, decimal=',')
# 选取其中一个列作为示例
df = df['MT_001']
# 处理数据:将数据按小时取平均值,并填补缺失值
df = df.resample('H').mean().fillna(method='ffill')
# 查看数据
print(df.head())
|
创建时间序列数据
创建时间序列数据,以便可以将其输入到LSTM模型中。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| # 创建时间序列数据
def create_dataset(data, time_step=1):
X, Y = [], []
for i in range(len(data) - time_step - 1):
a = data[i:(i + time_step)]
X.append(a)
Y.append(data[i + time_step])
return np.array(X), np.array(Y)
# 使用过去24小时的数据预测下一小时的消耗
time_step = 24
data = df.values
# 归一化数据
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler(feature_range=(0, 1))
data = scaler.fit_transform(data.reshape(-1, 1))
X, Y = create_dataset(data, time_step)
# 划分训练集和测试集
train_size = int(len(X) * 0.7)
test_size = len(X) - train_size
X_train, X_test = X[0:train_size], X[train_size:len(X)]
Y_train, Y_test = Y[0:train_size], Y[train_size:len(Y)]
# 重塑数据为 [样本, 时间步, 特征]
X_train = X_train.reshape(X_train.shape[0], X_train.shape[1], 1)
X_test = X_test.reshape(X_test.shape[0], X_test.shape[1], 1)
|
构建LSTM模型
使用 tensorflow 构建并训练LSTM模型。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, LSTM
# 构建LSTM模型
model = Sequential()
model.add(LSTM(50, return_sequences=True, input_shape=(time_step, 1)))
model.add(LSTM(50, return_sequences=False))
model.add(Dense(25))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mean_squared_error')
# 训练模型
model.fit(X_train, Y_train, batch_size=64, epochs=10, validation_data=(X_test, Y_test))
|
预测和可视化结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| # 预测
train_predict = model.predict(X_train)
test_predict = model.predict(X_test)
# 反归一化预测结果
train_predict = scaler.inverse_transform(train_predict)
test_predict = scaler.inverse_transform(test_predict)
Y_train = scaler.inverse_transform([Y_train])
Y_test = scaler.inverse_transform([Y_test])
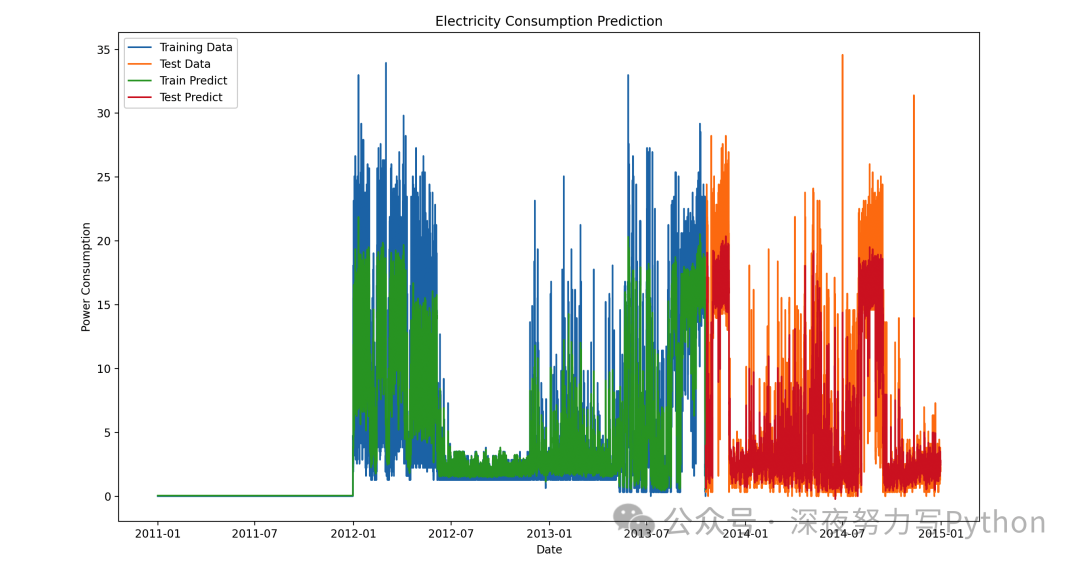
# 可视化结果
plt.figure(figsize=(14, 8))
plt.plot(df.index[:len(Y_train[0])], Y_train[0], label='Training Data')
plt.plot(df.index[len(Y_train[0]):len(Y_train[0]) + len(Y_test[0])], Y_test[0], label='Test Data')
plt.plot(df.index[:len(train_predict)], train_predict, label='Train Predict')
plt.plot(df.index[len(Y_train[0]):len(Y_train[0]) + len(test_predict)], test_predict, label='Test Predict')
plt.legend()
plt.xlabel('Date')
plt.ylabel('Power Consumption')
plt.title('Electricity Consumption Prediction')
plt.show()
|
模型优化
可以通过调整模型参数、使用更复杂的架构或更好的优化器来改进模型。
下面是一些改进模型的建议:
- 增加LSTM层的单元数量或层数。
- 使用不同的激活函数。
- 尝试不同的优化器,如AdamW。
- 使用交叉验证进行超参数调优。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| from tensorflow.keras.optimizers import Adam
# 构建优化后的LSTM模型
model_optimized = Sequential()
model_optimized.add(LSTM(100, return_sequences=True, input_shape=(time_step, 1)))
model_optimized.add(LSTM(100, return_sequences=True))
model_optimized.add(LSTM(100, return_sequences=False))
model_optimized.add(Dense(50))
model_optimized.add(Dense(1))
optimizer = Adam(learning_rate=0.001)
model_optimized.compile(optimizer=optimizer, loss='mean_squared_error')
# 训练优化后的模型
model_optimized.fit(X_train, Y_train, batch_size=64, epochs=20, validation_data=(X_test, Y_test))
# 预测并可视化结果
train_predict_optimized = model_optimized.predict(X_train)
test_predict_optimized = model_optimized.predict(X_test)
train_predict_optimized = scaler.inverse_transform(train_predict_optimized)
test_predict_optimized = scaler.inverse_transform(test_predict_optimized)
plt.figure(figsize=(14, 8))
plt.plot(df.index[:len(Y_train[0])], Y_train[0], label='Training Data')
plt.plot(df.index[len(Y_train[0]):len(Y_train[0]) + len(Y_test[0])], Y_test[0], label='Test Data')
plt.plot(df.index[:len(train_predict_optimized)], train_predict_optimized, label='Optimized Train Predict')
plt.plot(df.index[len(Y_train[0]):len(Y_train[0]) + len(test_predict_optimized)], test_predict_optimized, label='Optimized Test Predict')
plt.legend()
plt.xlabel('Date')
plt.ylabel('Power Consumption')
plt.title('Optimized Electricity Consumption Prediction')
plt.show()
|
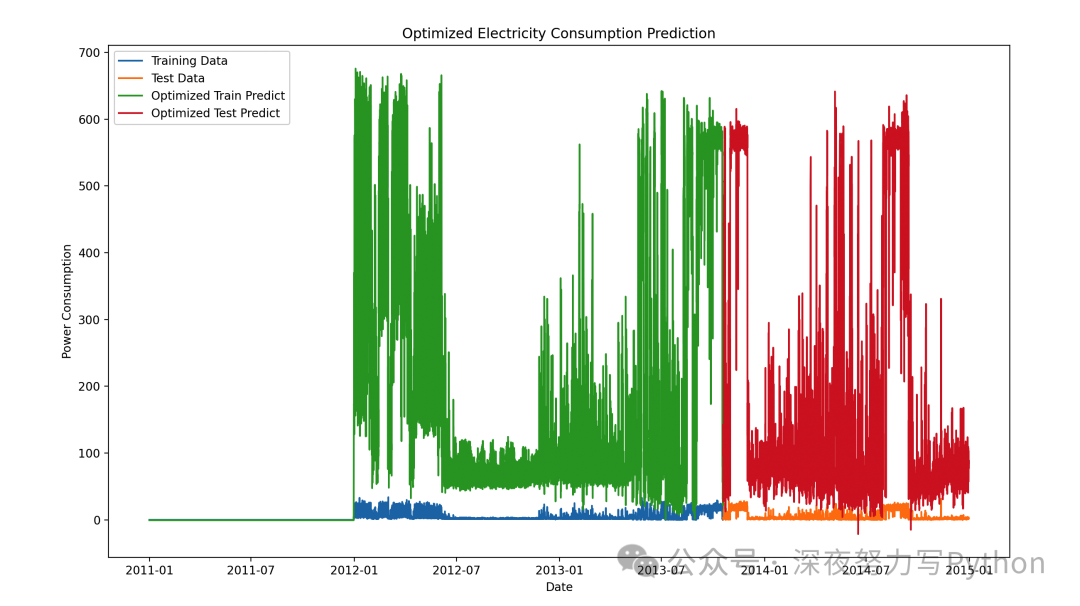
通过以上所有的步骤,咱们成功地构建并优化了一个LSTM模型,预测电力消耗,并对结果进行了可视化,更加容易接受~
模型分析
这里,咱们从模型的优缺点、以及与相似算法的对比,讨论在什么情况下该算法是优选,什么情况下可以考虑其他算法。
LSTM 模型 优缺点
优点
1. 处理长时间依赖性:LSTM可以有效地捕捉长时间依赖关系,在序列数据中能够记住和利用远距离的相关信息。
2. 梯度消失问题:通过门机制(遗忘门、输入门、输出门),LSTM解决了传统RNN中的梯度消失问题,使得模型在训练时更稳定。
3. 广泛适用:适用于各种时间序列数据,包括股票预测、天气预报、自然语言处理等。
缺点
1. 计算复杂度高:LSTM结构复杂,训练时间长,尤其在大数据集上,计算资源消耗较大。
2. 需要大量数据:LSTM需要大量的训练数据才能发挥出最佳效果,对小数据集的泛化能力较差。
3. 参数调优复杂:LSTM有较多的超参数,模型优化需要进行大量的实验和调优,过程复杂且耗时。
与相似算法的对比
LSTM vs. 简单RNN
- 优点:LSTM能更好地处理长时间依赖关系,解决了简单RNN中的梯度消失问题。
- 缺点:LSTM结构比简单RNN复杂,训练时间更长。
LSTM vs. GRU(门控循环单元)
- 优点:LSTM通过三个门(遗忘门、输入门、输出门)控制信息流动,理论上可以捕捉更复杂的依赖关系。
- 缺点:GRU只有两个门(更新门和重置门),结构较简单,计算量小于LSTM,但在很多实际应用中,GRU性能接近甚至优于LSTM。
LSTM vs. 一维卷积神经网络(1D-CNN)
- 优点:LSTM适用于序列数据,能捕捉时间上的依赖关系。
- 缺点:1D-CNN通过卷积操作捕捉局部时间特征,计算效率高于LSTM。在一些短时间依赖性较强的数据集上,1D-CNN可能表现更好。
选择LSTM的情境
适用场景
1. 长时间依赖关系:需要捕捉数据中长期的依赖关系时,如自然语言处理中的句子理解,气象数据中的季节变化。
2. 序列生成:生成类似文本、时间序列数据时,LSTM能够很好地建模数据的顺序和依赖关系。
3. 大数据集:在有足够多训练数据的情况下,LSTM能充分学习复杂的模式和特征。
考虑其他算法的情境
1. 短时间依赖关系:如果数据的依赖关系主要集中在短时间内,1D-CNN或简单RNN可能更适合。
2. 计算资源有限:在计算资源受限的情况下,GRU或1D-CNN的计算效率更高。
3. 小数据集:在数据量较小的情况下,较为简单的模型(如ARIMA,简单RNN)可能更适合,避免过拟合。
最后
LSTM在处理复杂的长时间序列数据方面表现出色,尤其适合需要捕捉长期依赖关系的任务。
但是,LSTM 复杂度和计算资源要求较高,需要大量的训练数据。与其他算法相比,LSTM在处理长时间依赖关系上有明显优势,但在短时间依赖关系或计算资源受限的情况下,其他算法如GRU、1D-CNN可能更为优选。